Indikatoren []

Der Vergleich von Messergebnissen ist auch ein guter Test, um das Verständnis der Lernenden über Messunsicherheiten zu überprüfen. Solche Datenvergleichsaufgaben sollten nicht auf eine Multiple-Choice-Frage (stimme zu/ stimme nicht zu) reduziert werden. Vielmehr sollte dies durch eine Begründung unterstützt werden.

Struktur von Begründungen []

Wenn man sich die Begründungen der Lernenden bei einer Datenvergleichsaufgabe ansieht, bestehen diese meistens aus einer bestimmten Vergleichsmaß, die verglichen wird, gefolgt von der Überprüfung eines bestimmten Vergleichskriteriums, das erfüllt (oder nicht erfüllt) ist. Die Betrachtung des Vergleichsmaßes und des Vergleichskriteriums, die von den Lernenden in ihren Begründungen genannt werden, gibt Aufschluss über das konzeptuelle Verständnis der Lernenden [1].

Für Lernende, die Datensätze vergleichen, wurden die folgenden Vergleichsmaße identifiziert

• Einzelner Wert: Die Lernenden vergleichen einzelne, isolierte Messungen (z. B. einen wiederkehrenden Wert oder einen Extremwert).
• Unsicherheit: Die Lernenden vergleichen nur die Unsicherheit.
• Paarweiser Vergleich: Die Lernenden vergleichen die Ergebnisse jeweils paarweise.
• Mittelwert: Die Lernenden vergleichen den Mittelwert.
• Abweichung: Die Lernenden subtrahieren zwei Datensätze und vergleichen die resultierenden Abweichungen.
• Datensatz: Die Lernenden vergleichen die Datensätze als Ganzes.
• Intervall: Die Lernenden vergleichen das gesamte Unsicherheitsintervall entweder als Bereich oder als Bestwert ± Unsicherheit.

Die folgenden Vergleichskriterien wurden identifiziert:

• Doppelte Werte: Die Lernenden suchen nach doppelten oder wiederkehrenden Werten.
• Größe: Die Lernenden vergleichen Größen und prüfen, ob die eine größer oder kleiner ist als die andere.
• Häufigkeit: Die Lernenden zählen das Auftreten bestimmter Ereignisse, z. B. wenn ein Wert größer/kleiner als der andere ist.
• Nähe: Lernende untersuchen, wie nahe oder ähnlich sich zwei Datensätze oder Messergebnisse sind.
• Überlappung: Lernende suchen nach Überschneidungen (oder dem Fehlen solcher) in ihren Datensätzen oder Messergebnissen.

Die Kombination dieses Vergleichsmaßes und des Vergleichskriteriums kann dem Point- und dem Set-Paradigma zugeordnet werden, siehe Abb. 10. Liegt die Kombination im roten Bereich, ist die Begründung dem Point-Paradigma zuzuordnen, liegt sie im grünen Bereich, kann die Begründung dem Set-Paradigma zugeordnet werden (zu Point- und Set-Paradigmen siehe Point und Set).

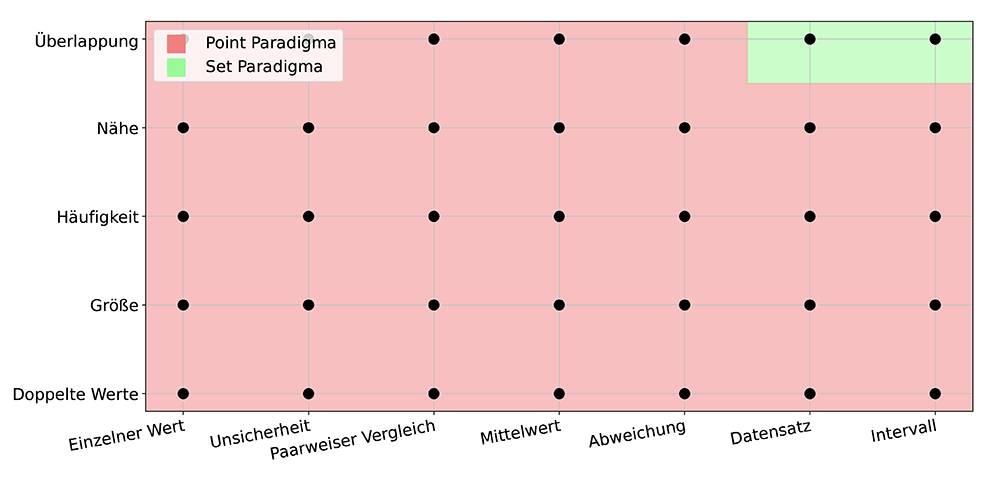
Abbildung 10: Die Kombination aus der zu Vergleichsmaß und dem Kriterium, das in einer Begründung geprüft wird, kann mit dem Point-Paradigma (rot) und dem Set-Paradigma (grün) in Verbindung gebracht werden.

Typische Antworten der Lernenden []

Angenommen, zwei Gruppen A und B messen die Fallzeit eines Objekts. Die Daten sind in Tab. 7 angegeben. Anhand der Daten soll die Frage beantwortet werden, ob die Fallzeiten gleich sind.

Tabelle 7: Zwei Datensätze, die auf Verträglichkeit verglichen werden können. Die untere Zeile zeigt den Mittelwert.

Fallzeit Gruppe A (s)	Fallzeit Gruppe B (s)
1,530	1,548
1,573	1,534
1,522	1,520
1,548	1,571
1,583	1,523
1,538	1,526
1,549	1,537

Eine typische Antwort der Lernenden könnte lauten:

"Die längste Fallzeit 1,583 s tritt in Gruppe A auf. Daher muss die Fallzeit des Objekts der Gruppe A größer sein."

Diese Person sucht nach dem größten (Vergleichskriterium: Größe) Wert in der Reihe (Vergleichsmaß: Einzelner Wert) und schließt daraus, dass die Gruppe, zu der dieser Wert gehört, die längste Fallzeit haben muss. Diese Person hat einen einzelnen Wert betrachtet, und das Kriterium ist, dass dieser Wert größer als die anderen Werte in der Reihe ist. Dieser einzelne Messwert bestimmt die Schlussfolgerung des Experiments. Dies steht in engem Zusammenhang mit dem Point-Paradigma, bei dem einzelne Werte repräsentativ für eine ganze Reihe sind.

Um diese Lernenden zu unterstützen, könnte man sie zunächst auffordern, darüber nachzudenken, warum eine Messreihe durchgeführt wird und was die Ursache für ihre Schwankungen ist. Auf diese Weise sollten die Lernenden erkennen, dass die Quellen der Messunsicherheit die Ergebnisse beider Gruppen beeinflussen. Dann kann man den Lernenden helfen, indem man sie die Streuung der gesamten Messreihe betrachten lässt.

Eine andere typische Antwort der Lernenden könnte lauten:

"Die Fallzeit des Objekts der Gruppe A ist länger, weil die Fallzeit der Gruppe A in der Regel länger ist als die der Gruppe B."

Diese Person hat die Messungen paarweise verglichen (Vergleichsmaß: paarweiser Vergleich) und geschaut, welcher der beiden Werte größer oder kleiner als der andere ist (Vergleichskriterium: Häufigkeit). Dies ist elaborierter als die vorherige Antwort, da alle Werte berücksichtigt werden. Der isolierte Vergleich von Messwertpaaren ist jedoch auch ein anschauliches Beispiel für Point-Paradigma-Schlussfolgerungen.

Es gibt mehrere Strategien, die den Lernenden helfen, ihre Überlegungen zu reflektieren. Man könnte die gleichen Messungen in einer anderen Reihenfolge anordnen und die Lernenden fragen, was ihre Schlussfolgerung ist. Die Lernenden werden schnell erkennen, dass sich ihre Schlussfolgerung mit ihrer Argumentation ändern muss. Oft reicht dies aus, damit die Lernenden ihre fehlerhafte Argumentation erkennen. Die Lernenden sollten dann angeleitet werden, die Messreihe als Ganzes zu betrachten. Eine hilfreiche Strategie ist es, die Ergebnisse in einem Diagramm darzustellen. Dies hilft ihnen, die Streuung des Datensatzes als Ganzes zu erkennen.

Eine weitere Antwort könnte lauten:

"Die beiden Mittelwerte, 1,549 s und 1,537 s, liegen sehr nahe beieinander, und daher können die beiden Zeiten als gleich angesehen werden."

Aus dieser Antwort wird deutlich, dass diese Person Mittelwerte verglichen hat (Vergleichsmaß: Mittelwert) und dass das Kriterium für die Übereinstimmung darin besteht, dass die Werte nahe genug beieinander liegen (Vergleichskriterium: Nähe). Obwohl der Vergleich des Mittelwerts als Set-Paradigma-Argumentation betrachtet werden könnte, tun Lernende dies oft als automatisierte Routine. Der Mittelwert selbst ist dann der einzige Wert, der berücksichtigt wird, sodass es sich um Point-Paradigma-Argumentation handelt. Die Annäherung der beiden Werte wird ebenfalls als Point-Paradigma-Argumentation betrachtet. Dies liegt daran, dass die Messunsicherheit berücksichtigt werden muss, damit eine Bewertung dieser Nähe hinsichtlich der Verträglichkeit erfolgen kann.

Um die Lernenden zu unterstützen, könnten Leitfragen in Betracht gezogen werden. Zum Beispiel könnte man sie fragen, was sie unter "nah" verstehen und was nah genug für die konkret bedeutet. Solange die Summe der Unsicherheiten beider Messgrößen kleiner ist als die Differenz zwischen den Mittelwerten, können die Ergebnisse immer noch als unverträglich angesehen werden.

Eine weitere Frage ist, welche Rolle der Mittelwert für die Lernenden spielt. Ist er ein Schätzwert für die Zentralität der Messreihe (Set-Paradigma-Argumentation) oder betrachten die Lernenden ihn als "Endergebnis" des Experiments (Point-Paradigma-Argumentation)? Wenn letzteres der Fall ist, könnte anschließend gefragt werden, was mit dem Mittelwert passieren würde, wenn eine weitere Messung zur Reihe hinzugefügt würde. Ein sich ändernder ⓘ "wahrer Wert"Hypothetisches Konstrukt, das ein exaktes wahres Ergebnis darstellen würde. ist aus Sicht des Point-Paradigmas problematisch, aber ein sich ändernder Bestwert innerhalb des Unsicherheitsintervalls ist aus Sicht des Set-Paradigmas unproblematisch.

Literatur

• Kok, K., & Priemer, B. (2023). Assessment tool to understand how students justify their decisions in data comparison problems. Physical Review Physics Education Research, 19(2), 020141. https://doi.org/10.1103/PhysRevPhysEducRes.19.020141