Handbuch

Unsicherheit []

Die Unsicherheit oder Messunsicherheit einer Messung ist eine Quantifizierung der Variabilität der Werte, die mit dem Ergebnis der Messung verbunden sein können. In den meisten Fällen folgen die Werte von wiederholten Messungen in einem Experiment der Normalverteilung. Daher ist es nicht verwunderlich, dass die Standardabweichung (oder die Standardabweichung des Mittelwerts) die gängigste wissenschaftliche Quantifizierung der Messunsicherheit ist.

Natürlich gibt es Messungen, bei denen keine Variabilität auftritt (zum Beispiel die Messung der Länge eines Tisches mit einem Maßband). Hier wird die Unsicherheit durch das Messinstrument bestimmt. Mehr Informationen dazu im Typ B.

Standardabweichung der Verteilung []

Die Standardabweichung der Verteilung ist der wissenschaftliche Standard zur Beschreibung der Variabilität einer Messgröße um ihren Mittelwert. Sie kann wie folgt berechnet werden: $$\sigma = \sqrt{\frac{1}{N}\sum_{i=1}^N(x_i-\bar{x})^2},\tag{2}$$ Dabei sind N die Anzahl der Messungen,xi die einzelnen Messwerte und x der Mittelwert der Messung.

Wenn die Daten normalverteilt sind, siehe Abb. 2, deckt die Fläche unter der Normalverteilung zwischen –σ und +σ, 68% der Gesamtfläche ab. Das bedeutet, dass 68% der Messungen im 1σ-Unsicherheitsintervall (d.h. im Wertebereich zwischen x – σ und x + σ) liegen werden. Für das 2σ-Intervall erhöht sich dieser Prozentsatz auf 95%.

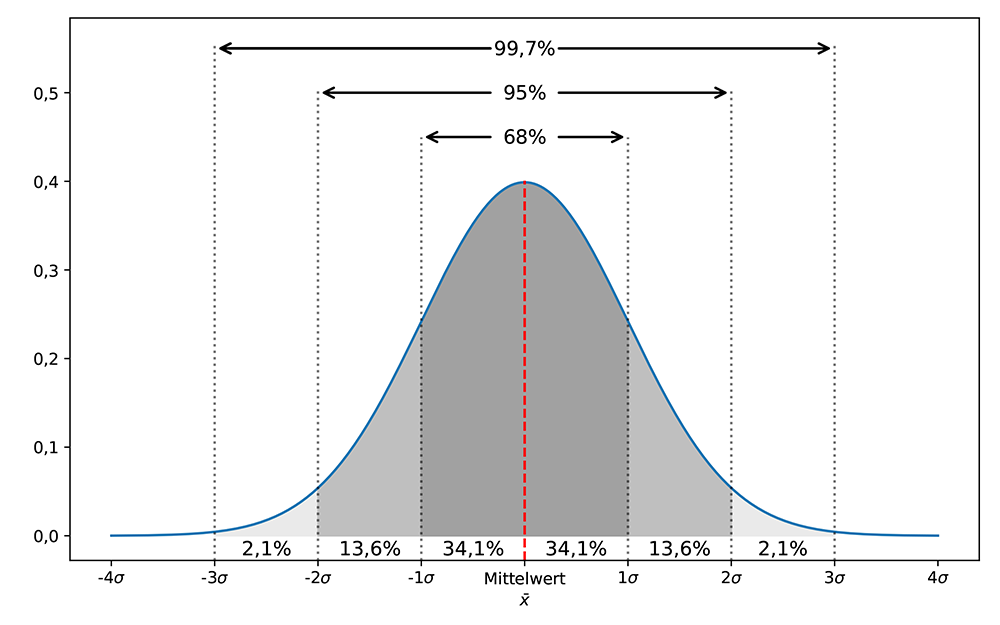
Abbildung 2: Eine Normalverteilung mit einem Mittelwert bei Null (rote gestrichelte Linie) und einer Standardabweichung σ. Die gestrichelten Linien zeigen die Grenzen von einem, zwei und drei Sigma an. Die prozentualen Angaben beschreiben den Anteil an Messwerten in dem entsprechenden Intervall.

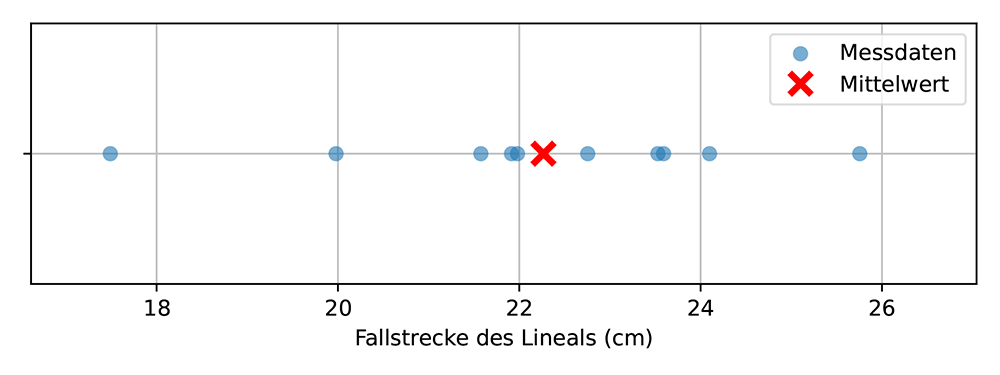
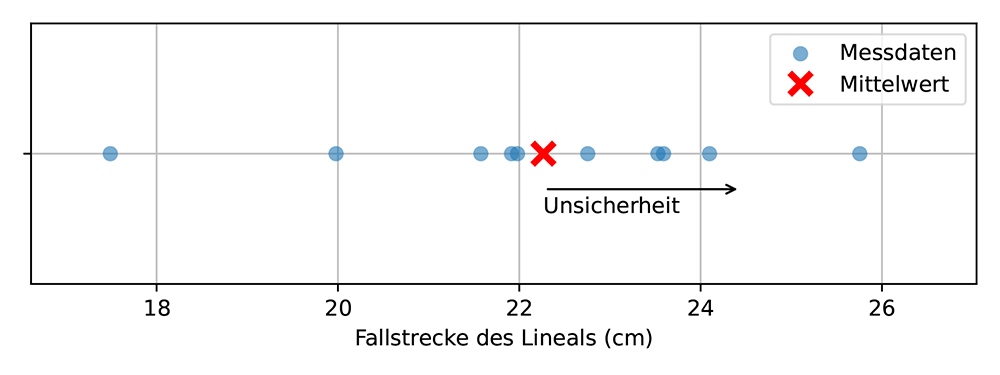
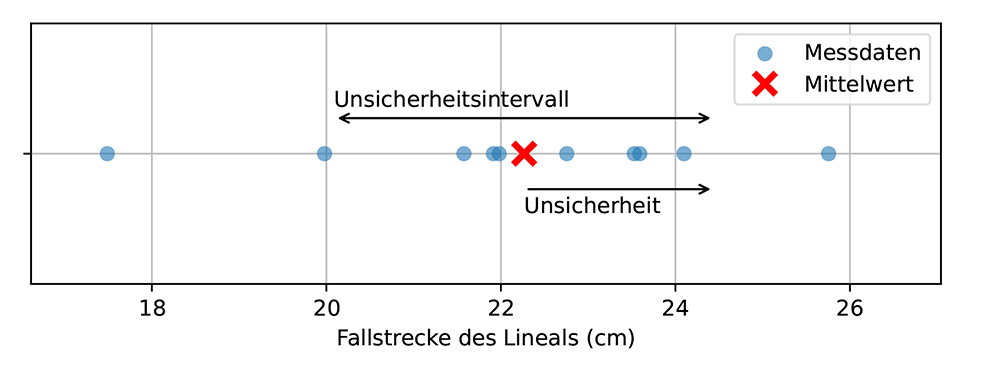
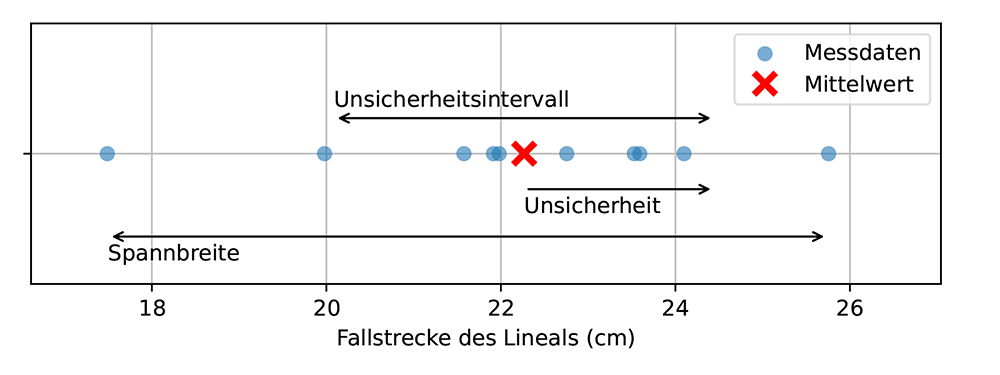
Betrachtet man wieder die Daten der Fallstrecke des Lineals, siehe Abb. 3a, so sind auch diese Daten mit einer Unsicherheit behaftet. Mit Hilfe der Gleichung (2) kann diese Unsicherheit berechnet werden, sie ist in Abb. 3b dargestellt, das Unsicherheitsintervall ist in Abb. 3c dargestellt. Da das Unsicherheitsintervall 68 % der Messungen umfasst, liegen nicht alle Messwerte innerhalb des Unsicherheitsintervalls. Abbildung 3d zeigt auch den gesamten Wertebereich, der alle Messungen umfasst.

1 / 4
(a) Zehn wiederholte Messungen der Fallstrecke eines Lineals.
2 / 4
(b) Die Unsicherheit dieses Datensatzes.
3 / 4
(c) Die Unsicherheit und das Unsicherheitsintervall.
4 / 4
(d) Der Spannbreite, der Unsicherheit und dem Unsicherheitsintervall.
❮ ❯

Abbildung 3: Messdaten der Fallstrecke eines Lineals, wie in Abb. 1 jetzt mit der Unsicherheit.

Standardabweichung des Mittelwerts []

Die Standardabweichung des Mittelwerts gibt, wie der Name bereits andeutet, die Messunsicherheit des Mittelwerts an (und nicht die Messunsicherheit der einzelnen Messungen). $$\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{N}}.\tag{3}$$

Die Standardabweichung des Mittelwerts wird manchmal auch als Standardfehler bezeichnet. Aufgrund der unpassenden Konnotation des Wortes Fehler wird die Verwendung des Begriffs Standardabweichung des Mittelwerts oder Standardunsicherheit bevorzugt.

Im Gegensatz zur Standardabweichung einer Verteilung wird die Standardabweichung des Mittelwerts mit zunehmender Zahl der Messungen kleiner. Konzeptionell ist dies zu verstehen, weil mit zunehmender Anzahl von Messungen, auch wenn sie mit großen Messunsicherheiten behaftet sind, die zugrunde liegende Verteilung immer deutlicher wird. Aus dieser Verteilung kann das Zentrum (der Mittelwert) mit größerer Sicherheit bestimmt werden.

Alltagsvorstellungen zur Messunsicherheit []

Viele Lernende sehen Messunsicherheiten als etwas an, das in einem Experiment eliminiert werden kann [1–3]. Dies hängt stark mit dem Glauben an die Existenz eines ⓘ "wahren Wertes"Hypothetisches Konstrukt, das ein exaktes wahres Ergebnis darstellen würde. zusammen, siehe wahrer Wert. Einige Lernende glauben, dass die Messunsicherheit mit genügend Übung auf Null reduziert werden kann, andere glauben, dass dies nur mit "echten" Messinstrumenten möglich ist, wieder andere denken, dass dies nur von "professionellen" Wissenschaftler*innen erreicht werden kann. Wie auch immer diese Vorstellungen sind: Messunsicherheiten werden immer in jedem Experiment auftauchen. Sie sind in jedem Experiment vorhanden und ungleich null.

Einige Lernende und sogar Lehrbücher bezeichnen Messunsicherheiten als "Fehler". Es ist bekannt, dass die Verwendung dieses Wortes die Lernenden zu der Annahme verleitet, dass sie etwas falsch gemacht haben [3–8]. Auch der Guide to the Uncertainty of Measurements (kurz GUM [9]) verzichtet ausdrücklich auf die Verwendung des Begriffs "Fehler". Das Wort "Fehler" steht im Zusammenhang mit Messunsicherheiten für einen tatsächlichen Fehler: einen (nicht behebbaren) Fehler oder etwas, das schief gelaufen ist. Messunsicherheiten hingegen gehören zu jedem wissenschaftlichen Experiment und lassen sich nicht vermeiden.

Die Allgegenwart von Messunsicherheiten und die Vorstellung, dass alle Wissenschaftler*innen damit umgehen müssen—und die daraus resultierende Ungewissheit—kann ein beruhigender Gedanke für die Lernenden sein. Es zeigt ihnen, dass sie nicht etwas falsch machen, sondern sich in einer authentischen wissenschaftlichen Praxis bewegen. Dadurch entwickelt sich gleichzeitig eine angemessene Sicht auf das Wesen der Naturwissenschaft [10–12].

Hierbei ist wichtig zu beachten, dass die Standardabweichung in der Sekundarstufe I zu komplex oder zeitaufwändig sein könnte (Alternativen werden später in Typ A diskutiert).Folgendes häufiges Missverständnis soll hier noch richtiggestellt werden:

die Auffassung dass mehr Messungen zu einer geringeren Standardabweichung führen [13]. Dies ist jedoch nicht der Fall. Mehr Messungen (xi) führen nicht zu einem kleineren Wert der Standardabweichung (σ), siehe Gleichung (2). Vielmehr erhält man mit mehr Messungen eine bessere Beschreibung der Verteilung der Messwerte, d.h. die Form der Normalverteilung wird deutlicher. Die Breite der Verteilung ändert sich jedoch nicht. Im gegensatz dazu gilt: die Standardabweichung des Mittelwertes (σ x) wird jedoch kleiner. Diese Quantifizierung ist den Lernenden jedoch nicht immer bekannt, oder sie können begrifflich nicht zwischen den beiden unterscheiden.

Literatur