Handbuch

Mittelwert []

Das arithmetische Mittel einer Reihe von Messungen kann wie folgt berechnet werden: $$\bar{x} = \frac{1}{N}\sum_{i=1}^N x_i, \tag{1}$$ wobei N die Anzahl der wiederholten Messungen ist und xi die einzelnen Messwerte sind.

Dieser Mittelwert gilt als der Bestwert des Wertes der Messgröße aus einer Reihe von Messungen—der zentralste Punkt der Messreihe. Man kann es sich auch so vorstellen: Wenn man raten müsste, wie die nächste Messung ausfallen würde, liegt dieser Mittelwert—im Durchschnitt—am nächsten an dieser neuen Messung.

Dies deckt sich mit der Vorstellung, dass man mit dem Messen aufhören kann, wenn sich dieser Mittelwert (und die Unsicherheit) stabilisiert hat. Zu diesem Zeitpunkt stimmt dieser Mittelwert mit dem zentralsten Wert der Messungen überein, die das Experiment hervorbringt.

Das arithmetische Mittel wird meist als der Bestwert der Messgröße verwendet. Es gibt jedoch auch alternative Mittelwerte. Eine Möglichkeit ist die Verwendung des ⓘ MediansDer mittlere Wert in einer Reihe von sortierten Messwerten.: der mittlere Wert eines sortierten Datensatzes. Ein anderes Maß ist der ⓘ ModusDer am häufigsten auftretende Wert in einer Reihe von Messwerten.: die Messung, die am häufigsten auftritt. In dem Fall, dass wiederholte Messungen alle genau das gleiche Ergebnis liefern, ist der Bestwert schließlich nur dieser eine Wert.

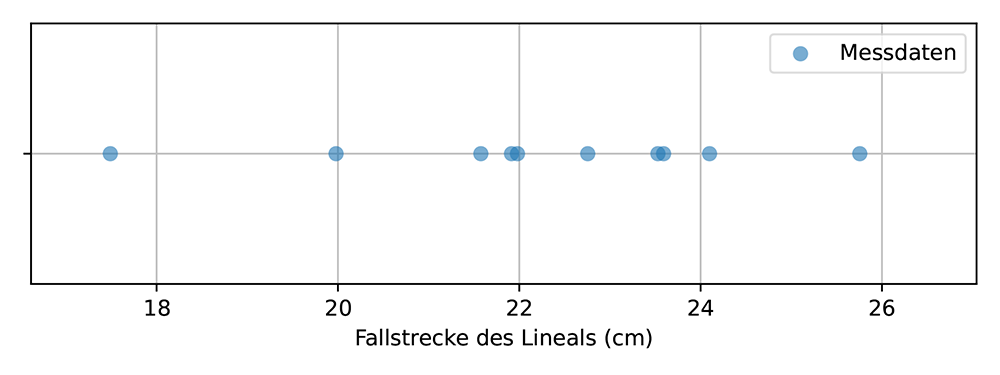
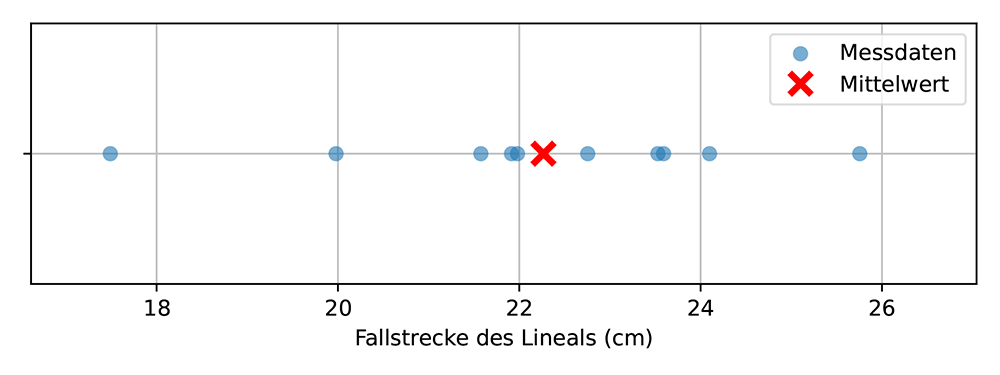
Angenommen, man möchte die Reaktionszeit einer Person messen. Dazu kann man die Fallstrecke eines Lineals messen, siehe Abb. 1a. Mit Hilfe der Gleichung h = 1/2 g t2 kann die Reaktionszeit bestimmt werden. Die gemessenen Daten werden in Abbildung 1b grafisch dargestellt. Der Mittelpunkt dieser Messungen ist der Mittelwert, der in Abb. 1c als rotes Kreuz dargestellt ist.

1 / 3
(a) Messung der Fallstrecke eines Lineals zur Bestimmung der Reaktionszeit.
2 / 3
(b) Zehn wiederholte Messungen der Fallstrecke eines Lineals.
3 / 3
(c) Der Mittelwert (rotes Kreuz) ist der zentralste Punkt in diesem Datensatz.
❮ ❯

Abbildung 1: Messdaten eines Experiments, bei dem die Reaktionszeit durch Messung der Fallstrecke eines Lineals bestimmt wird.

Alltagsvorstellungen über den Mittelwert []

Die Berechnung des Mittelwerts stellt für die Lernenden normalerweise kein Problem dar. Allerdings bleiben die Überlegungen der Lernenden darüber, was der Mittelwert repräsentiert, oft oberflächlich [1, 2].

Manchmal wird der Mittelwert als Grund für die Durchführung wiederholter Messungen genannt. Da man natürlich mehrere Messungen durchführen muss, um einen Mittelwert zu berechnen [3], ist dies oft ein routinemäßiges und automatisiertes Verfahren, und der Mittelwert wird anschließend als isolierter Wert betrachtet. Einige Lernende gehen sogar noch weiter und betrachten diesen Wert als ⓘ "wahren Wert"Hypothetisches Konstrukt, das ein exaktes wahres Ergebnis darstellen würde. [4]. Obwohl der Prozess der Berechnung eines Mittelwerts aus einer Reihe von wiederholten Messungen mit dem Set-Paradigma in Verbindung gebracht werden kann, wird die Betrachtung des Mittelwerts als isolierter Wert als Point-Paradigma betrachtet [5]. Um zu einer adäquaten Argumentation im Set-Paradigma zu gelangen, müssen die Lernenden den Mittelwert um die Messunsicherheit ergänzen.

Eine weitere Vorstellung über den Mittelwert ist die, dass er "präziser" ist [6]. Obwohl ein (stabilisierter) Mittelwert die beste Schätzung des Wertes der Messgröße ist, sagt dies nichts über die Präzision aus, die durch die Messunsicherheit angegeben wird.

Literatur