Ergebnisse Vergleichen [
]
Bisher lag der Schwerpunkt auf den Quellen der Messunsicherheit, ihrer Auswirkung auf die Daten, ihrer Quantifizierung und ihrer Fortpflanzung. In diesem Abschnitt geht es um die Anwendung der Messunsicherheit.
Messunsicherheiten sind keine Belastung, die am Ende eines Experiments berechnet werden müssen—zumindest sollten sie es nicht sein! Messunsicherheiten sind nützlich, weil sie den Vergleich von Messergebnissen ermöglichen. Es wäre Zufall, wenn zwei Mittelwerte von zwei verschiedenen Messreihen genau gleich sind. Das bedeutet aber nicht, dass zwei Ergebnisse nur dann miteinander verträglich sind. Für einen korrekten Vergleich müssen die Unsicherheitsintervalle berücksichtigt werden.
Dieser Teil behandelt einige praktische Regeln für den Vergleich von Messergebnissen im Allgemeinen und wie Lernende dabei vorgehen können.
Der Vergleich von zwei Messergebnissen ist Praxis in der Wissenschaft. Hierbei kann nicht ohne Berücksichtigung der Messunsicherheit vorgegangen werden.
Eine Möglichkeit, zwei Mittelwerte zu vergleichen, besteht in der Berechnung eines t-Tests. Das mathematische Verfahren dieser Test würde aber den Rahmen dieser Einheit sprengen und für den Unterricht ungeeignet. Der Test vergleicht jedoch die beiden Mittelwerte, berücksichtigt ihre jeweilige Varianz sowie die Anzahl der wiederholten Messungen und bestimmt den Grad der Überschneidung zwischen ihnen.
Vergleich von Unsicherheitsintervallen []
Für den Vergleich von Datensätzen oder Messergebnissen im schulischen Kontext ist ein t-Test oftmals zu kompliziert. Daher muss die Vergleichsmethode vereinfacht werden. Dies kann durch den Vergleich von Unsicherheitsintervallen geschehen (siehe Gl.(8) in Unsicherheit). Eine Faustregel besagt, dass sich überlappende Unsicherheitsintervalle auf verträgliche Ergebnisse hinweisen.
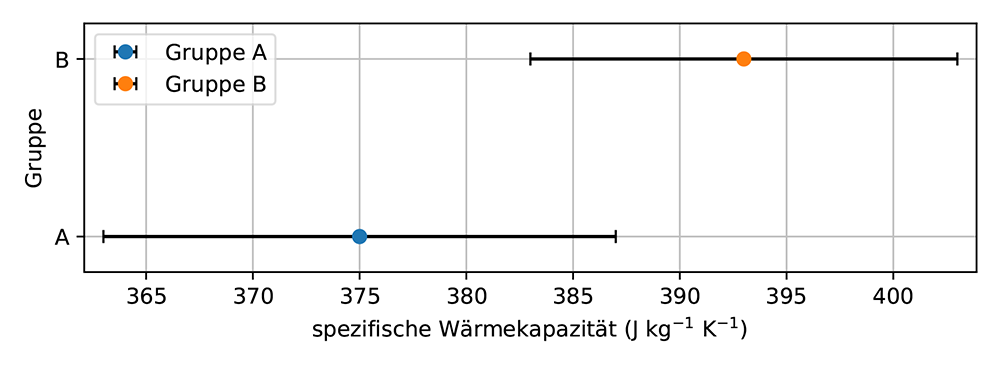
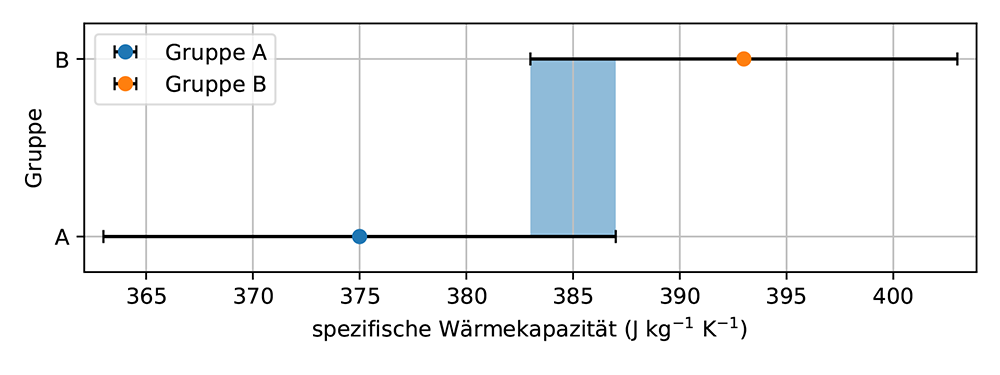
Angenommen zwei Gruppen haben die spezifische Wärmekapazität von zwei ähnlich aussehenden Metallobjekten gemessen. Gruppe A hat cA = (375 ± 12) J kg-1 K-1 gemessen und Gruppe B cB = (393 ± 10) J kg-1 K-1, siehe Abb. 9a. Die Gruppen fragen sich nun: Könnte das Metall der beiden Objekte das gleiche sein, also die gleiche spezifische Wärmekapazität haben? Das Unsicherheitsintervall gibt den Bereich an, in dem die Messgröße zu erwarten ist. Die Überlappung der Unsicherheitsintervalle deutet also auf einen gemeinsamen Bereich möglicher spezifischer Wärmekapazitäten hin, die beiden Objekten zugeordnet werden können, siehe Abb. 9b. Daher sind die Ergebnisse verträglich und die Gruppen müssen die Möglichkeit berücksichtigen, dass die spezifische Wärmekapazität der beiden Objekte gleich ist.
Abbildung 9: Die Messergebnisse der spezifischen Wärmekapazität, gemessen von den Gruppen A und B.
Das bedeutet nicht, dass sie bewiesen haben, dass die spezifische Wärmekapazität dieselbe ist! Sie haben einen Hinweis für die Möglichkeit, dass sie dieselbe sein könnte. Je nach Grad der Überschneidung und dem Bereich des Unsicherheitsintervalls kann diese Möglichkeit bewertet werden.
Alltagsvorstellungen zum Vergleich von Daten []
Auf die Frage nach der Verträglichkeit zwischen einem Messergebnis und einem Referenzwert verweisen einige Lernende auf die (prozentuale) Differenz. Dies ist zwar ein Aspekt der Qualität eines Ergebnisses, aber kein Hinweis auf die Verträglichkeit. Dies kann den Lernenden anhand der Ergebnisse in Tab. 6 verdeutlicht werden.
Tabelle 6: Experimentelle Ergebnisse bei der Bestimmung der Erdbeschleunigung. Das Messergebnis A hat zwar die geringste Unsicherheit, ist aber nicht verträglich mit dem Referenzwert.
| Referenzwert: | |
| gRef | 9,81 m/s2 |
| Messergebnisse: | |
| gA | (9,83 ± 0,01) m/s2 |
| gB | (9,78 ± 0,05) m/s2 |
| gC | (9,83 ± 0,15) m/s2 |
Obwohl die Gruppen A und C beide eine Differenz von 0,02 m/s2 zum Referenzwert aufweisen, ist das Ergebnis der Gruppe A nicht verträglich mit dem Referenzwert. Die Gruppen B und C sind beide mit dem Referenzwert verträglich. Und obwohl die Differenz zum Referenzwert bei Gruppe B größer ist als bei Gruppe C, ist ihre Unsicherheit dreimal kleiner.
Weitere Lektüre [
]
Für eine didaktische Reduktion des t-Tests siehe [1].
Ein Online-Rechner für den t-Test findet sich hier: https://www.graphpad.com/quickcalcs/ttest1.cfm.
Weitere Erklärungen zur Statistik des t-Tests findet man bei Wikipedia: https://en.wikipedia.org/wiki/Student's_t-test.
Literatur
- Neumann, S. (2021). Bin ich wirklich schneller als mein Sitznachbar? Plus Lucis, 4, 36–38.