Handbuch

Messergebnis []

Da Messunsicherheiten die Qualität eines Experiments anzeigen, ist kein Messergebnis ohne die Angabe der Unsicherheit vollständig. Im Folgenden werden die verschiedenen Möglichkeiten zur Angabe des Messergebnisses aufgezeigt, gefolgt von den Regeln für die Anzahl der signifikanten Ziffern, die angegeben werden müssen.

Dokumentation von Messergebnissen []

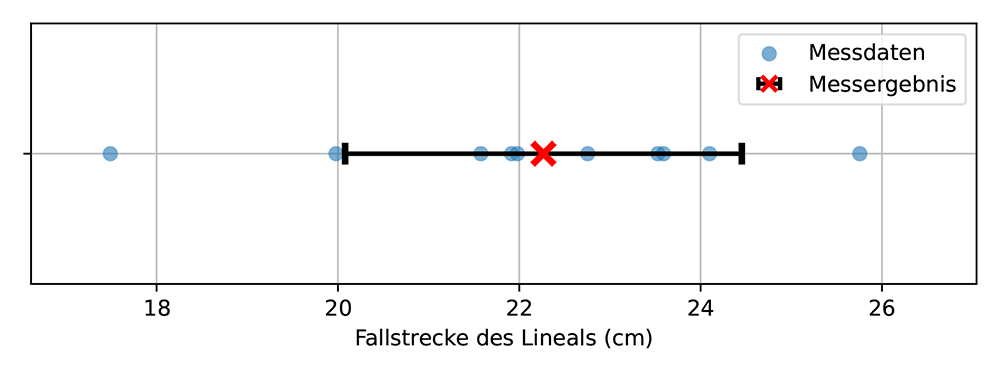
Ein vollständiges Messergebnis gibt immer den Bestwert und die Messunsicherheit an. Meist wird dies wie folgt angegeben: $$\text{Messergebnis} = \text{Bestwert} \pm \text{Messunsicherheit}.\tag{5}$$ Der Bestwert ist meist der Mittelwert x, und die Messunsicherheit die Standardabweichung σ.

Die Rundung des Bestwertes hängt von der Anzahl der Ziffern der Unsicherheit ab. Der Bestwert erhält genauso viele Dezimalstellen, wie die Unsicherheit. Ein Beispiel: Ein Strom wird gemessen: I = 0,227 459 A mit einer Unsicherheit uI = 0,0050 A, siehe Abb. 4. Die Unsicherheit hat vier Dezimalstellen, daher wird der Bestwert auf vier Dezimalstellen gerundet: $$I=(0{,}2275 \pm 0{,}0050)\text{ A}.\tag{6}$$

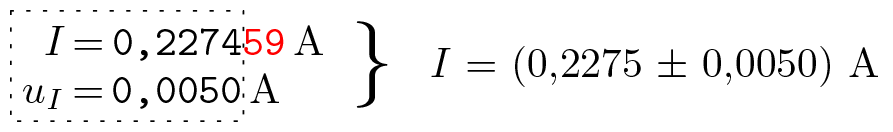
Abbildung 4: Der Bestwert des Stroms wird entsprechend der Unsicherheit des Stroms gerundet, d. h. auf vier Dezimalstellen.

Eine weitere Möglichkeit, Unsicherheit zu kennzeichnen, besteht darin, sie in Klammern zu setzen. Dies lässt sich am besten anhand des obigen Beispiels veranschaulichen. Durch die Schreibweise in Klammern wird dies zu: $$I=0{,}2275(50)\text{ A}.\tag{7}$$ Diese Schreibweise ist für Lernende etwas weniger intuitiv. Die DIN bevorzugt diese Notation für die Industrie, da sie sich von der Toleranz abgrenzt, die die gleiche Notation wie (6) hat. Die Toleranz gibt die maximale Abweichung zwischen Messungen und einem Referenzwert an, die z.B. in Produktionsprozessen erlaubt ist.

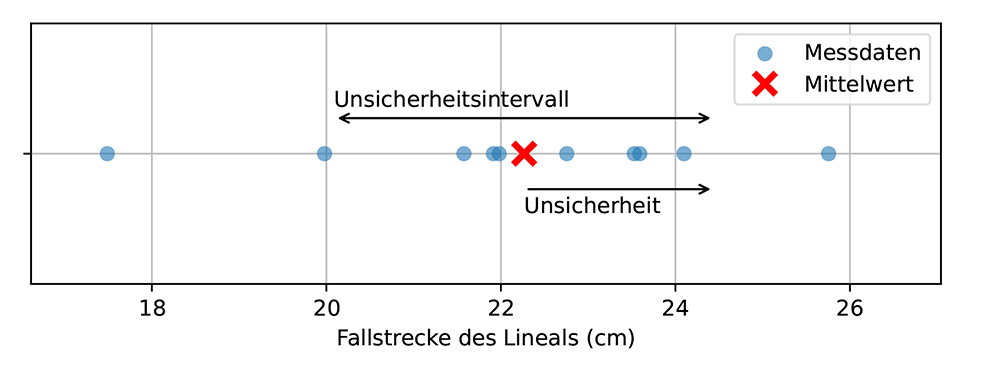
Die Messunsicherheit ist ein Hinweis auf die Genauigkeit eines Messergebnisses und damit ein Hinweis auf die Qualität des Experiments. Die Messunsicherheit erstreckt sich über ein ⓘ UnsicherheitsintervallDer Wertebereich, der durch den Mittelwert und die Unsicherheit aufgespannt wird. um den Bestwert. Das Unsicherheitsintervall reicht von: $$\text{Unsicherheitsintervall} = [\bar{x}-\sigma ; \bar{x}+\sigma].\tag{8}$$ Das Unsicherheitsintervall kann als der Bereich von Werten angesehen werden, in dem die Messgröße (mit einem bestimmten Grad des Vertrauens) zu erwarten ist.

Betrachtet man wieder die Messdaten der Fallstrecke eines Lineals, siehe Abb. 5a, so kann dieses Messergebnis grafisch dargestellt werden. Die Standardmethode zur Darstellung dieses Ergebnisses ist die Verwendung von Unsicherheitsbalken (manchmal auch als Fehlerbalken bezeichnet), wie in Abb. 5b gezeigt. Es ist zu beachten, dass in diesem Fall die Unsicherheit für die Variable auf der x-Achse dargestellt wird, während für die Unsicherheiten auf der y-Achse die Unsicherheitsbalken vertikal verlaufen.

1 / 2
(a) Die Unsicherheit und das Unsicherheitsintervall.
2 / 2
(b) Die grafische Darstellung des Messergebnisses.
❮ ❯

Abbildung 5: Messdaten der Fallstrecke eines Lineals, wie in Abb. 1 jetzt mit volständiges Messergebniss.

Anzahl der signifikanten Ziffern []

Im Beispiel von vorhin wurde die Messunsicherheit des Stroms mit zwei ⓘ signifikante ZiffernDie Anzahl der Ziffern nach den führenden Nullen. angegeben. Die Anzahl signifikante Ziffern ist die Anzahl der Ziffern ohne führende Nullen, siehe Tab. 3.

Tabelle 3: Die Anzahl der signifikanten Ziffern in blau für bestimmte Größen.

Größe signifikante Ziffern
\(l= \textcolor{blue}{17{,}2}\text{ cm}\) 3
\(t = \textcolor{blue}{10{,}02}\text{ s}\) 4
\(V = 0{,}0\textcolor{blue}{250}\text{ L} = \textcolor{blue}{25{,}0}\text{ mL}\) 3
\(\lambda = \textcolor{blue}{640{,}0}\text{ nm} = \textcolor{blue}{6{,}400}\cdot 10^{-7}\text{ m}\) 4
\(d = 0{,}000\,0\textcolor{blue}{10}\text{ m} = \textcolor{blue}{10}\cdot 10^{-6}\text{ m} = 0{,}0\textcolor{blue}{10}\text{ mm}\) 2

Die Anzahl der signifikanten Ziffern der Messunsicherheit bestimmt die Anzahl der signifikanten Ziffern der besten Schätzung, die entsprechend der Messunsicherheit gerundet wird, siehe Abb. 4. Es ist zu beachten, dass die Anzahl der signifikanten Ziffern des Bestwertes immer größer oder gleich der Anzahl der signifikanten Ziffern der Messunsicherheit ist. Es gibt drei Regeln für die Anzahl der signifikanten Ziffern der Messunsicherheit:

Der GUM [siehe 1] bevorzugt keine spezifische Regel für die Anzahl der signifikanten Ziffern der Unsicherheit. Jedoch wird angemerkt, dass maximal zwei Ziffern zu verwenden sind.

Für die Rundung der Messunsicherheit gibt es zwei Möglichkeiten: normales Runden (wie oben) oder Aufrunden. Ein konsequentes Aufrunden (z. B. 0,005 01 A = 0,0051 A oder sogar 0,005 01 A = 0,006 A) ist ein sehr konservatives Verfahren, das zu Überschätzungen der Unsicherheit führen kann. Der GUM ist hier nicht eindeutig, scheint aber die normale Rundung zu bevorzugen. Es wird betont, dass es manchmal angemessen ist, Unsicherheiten mit gesundem Menschenverstand aufzurunden. Dies würde bedeuten, u = 0,029 48 L auf 0,0030 L aufzurunden, aber u =0,005 01 A auf 0,0050 A abzurunden.

Alltagsvorstellungen über das Messergebnis []

Auf die Frage, wie ein Messergebnis angegeben werden sollte, geben viele Lernende (selbst auf Universitätsebene) an, dass der Mittelwert angegeben werden sollte [2]. Für ein vollständiges Messergebnis sollte dieser jedoch durch die Unsicherheit ergänzt werden. Um die Lernenden zum Nachdenken darüber anzuregen, könnte man sie fragen, wie ihr Messergebnis die Qualität ihres Experiments widerspiegelt.

Literatur