Graphen []

Manchmal erfolgt die Bestimmung einer Größe nicht durch wiederholte Messungen, sondern durch die Betrachtung der Abhängigkeit zwischen zwei anderen Variablen. In diesem Fall können die Daten mit Hilfe eines Diagramms und einer Trendlinie oder einer Fitfunktion ausgewertet werden.

Bestimmung der Unsicherheit einer Fitfunktion []

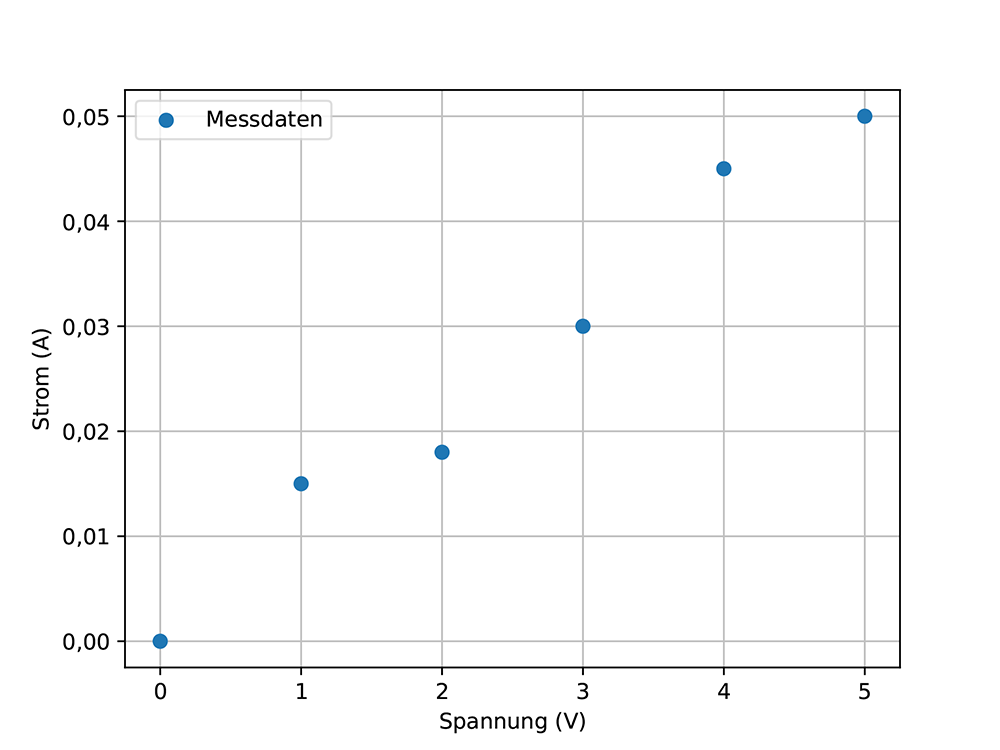
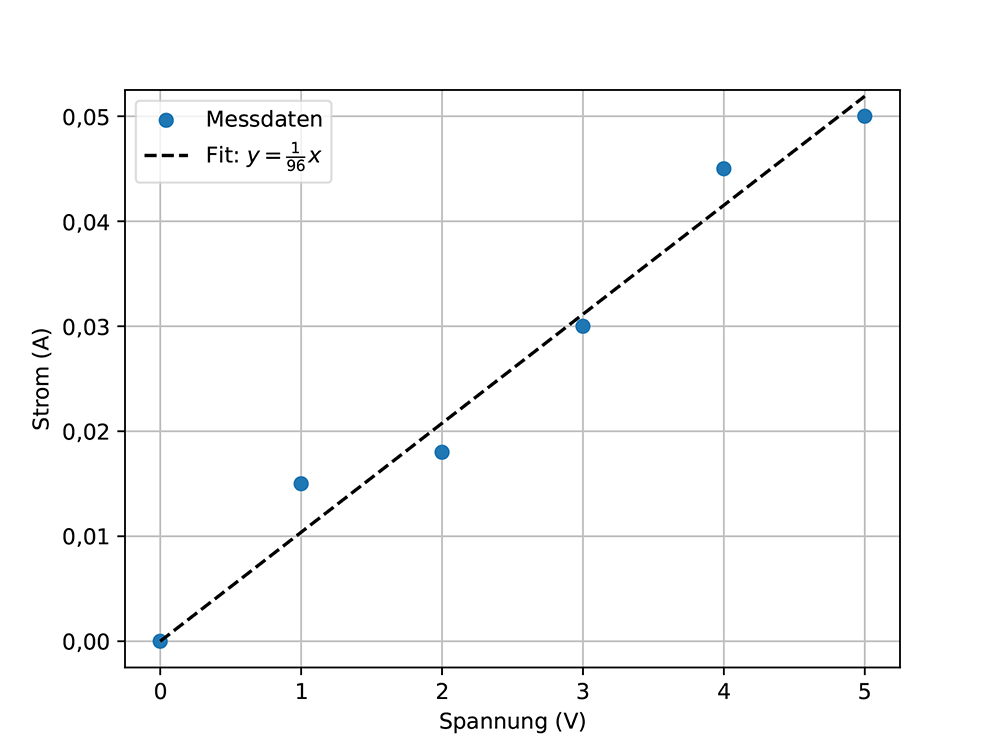
Angenommen, man möchte den Widerstand eines Widerstands R bestimmen. Dazu kann man die Spannung U variieren und messen und den resultierenden Strom I messen. Die verschiedenen Messungen können in einem (U,I)-Diagramm aufgetragen werden, siehe Abb. 8a. Eine lineare Trendlinie (Fit) der Form y = ax + b kann an die Daten angepasst werden, siehe Abb. 8b. Die meisten Computerprogramme (Excel, Qti-Plot, Google Sheets, ...) verwenden die Methode der kleinsten Quadrate. Das Ergebnis dieses Verfahrens liefert die Steigung a und (wenn gewünscht) den y-Achsenabschnitt b.

Unter Verwendung des Ohm'schen Gesetzes I = U/R kann man den Widerstand anhand der Steigung a berechnen, die gleich 1/R ist. In diesem Fall wird der Widerstand zu 96,3 Ω berechnet.

1 / 4

(a) Ein (U,I)-Diagramm von einigen Messdaten.

2 / 4

(b) Das (U,I)-Diagramm mit einem linearen Fit, welcher durch den Ursprung gezwungen wird. Die Steigung des Fits ist gleich 1/R. Es kann kein Schluss auf die Angemessenheit der linearen Passung bzgl. der Messdaten gezogen werden.

3 / 4

(c) Dasselbe (U,I)-Diagramm, aber jetzt mit Messunsicherheiten (durch Kästchen gekennzeichnet). Diese Darstellung zeigt, dass die Anpassung mit allen Messungen übereinstimmt.

4 / 4

(d) Das gleiche (U,I)-Diagramm, aber jetzt mit maximaler und minimaler Steigung, die durch alle Unsicherheitsfelder gehen. Diese Steigungen können verwendet werden, um die Unsicherheit der Steigung zu bestimmen.

❮ ❯

Abbildung 8: Verschiedene Darstellungen von Messdaten der Spannung am und des Stroms durch einen Widerstand.

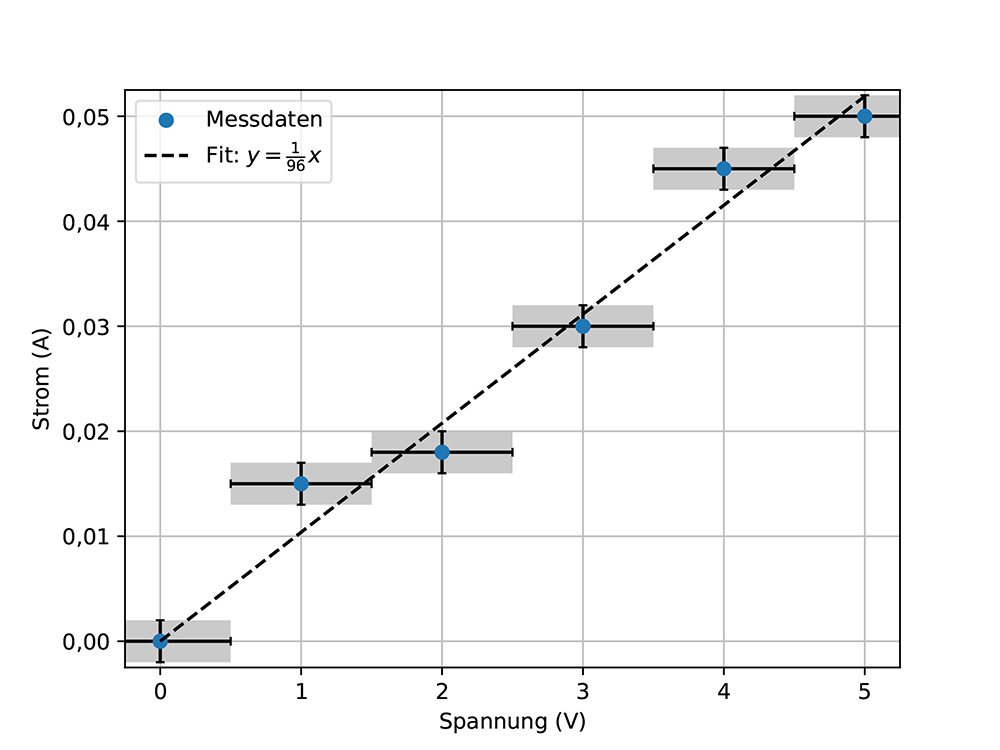
Dieses Diagramm zeigt jedoch nicht, ob der Fit wirklich zu den Daten "passt". Dies lässt sich nur feststellen, wenn man die Messunsicherheit betrachtet, siehe Abb. 8c. Diese Abbildung zeigt, dass die Anpassung durch alle Unsicherheitsfelder (die grau schattierten Bereiche, die durch die Unsicherheit der Spannung und des Stroms aufgespannt werden) geht und somit eine gute Anpassung an die Daten darstellt. An diesem Punkt könnte man sagen, dass der Widerstand des Widerstands einen Bestwert von R = 96,3 Ω hat.

Um die Messunsicherheit der Fitfunktion zu bestimmen, kann man auf die Methode der kleinsten Quadrate zurückgreifen und diese berechnen. Dies würde u_R = 3,7 Ω ergeben, also R = (96,3 ± 3,7) Ω. Die genaue Berechnung würde jedoch den Rahmen dieser Einheit sprengen.

Alternative grafische Unsicherheitsermittlung []

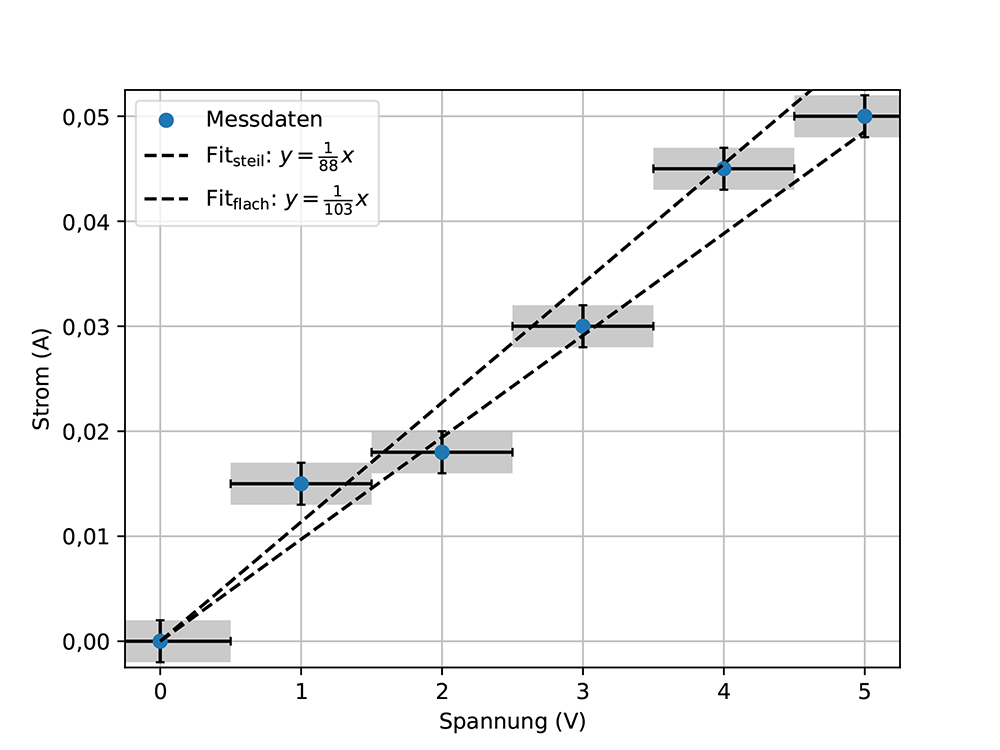
Es gibt eine vereinfachte, grafische Methode zur Bestimmung der Unsicherheit. Dazu zeichnet man die steilste und die flachste Fitfunktion, die noch durch alle Unsicherheitsfelder gehen und bestimmt deren Steigungen, siehe Abb. 8d. Daraus ergibt sich eine Steigung mit Widerständen von R = 88 Ω und R = 103 Ω. Unter Verwendung desselben Verfahrens, das für die maximale Abweichung verwendet wurde (siehe Gl. (9)), ergibt sich eine Messunsicherheit von u_R = 8 Ω, sodass R = (96 ± 8) Ω.

In diesem Beispiel wird die Messunsicherheit durch diese Methode eindeutig überschätzt. In anderen Fällen, wenn die Messunsicherheiten pro Datenpunkt klein sind, liefert diese Methode zu kleine Messunsicherheiten. Manchmal scheint die Methode überhaupt nicht zu funktionieren, da es keine Linie gibt, die durch alle Unsicherheitsfelder geht. In diesen Fällen ist es wichtig, sich daran zu erinnern, dass auch die Methode der kleinsten Quadrate nicht durch alle Unsicherheitsfelder geht, aber dennoch ein Ergebnis liefert. Man sollte eine Linie zeichnen, die so gut wie möglich durch die Unsicherheitsboxen geht. Die steilsten und flachsten Steigungen sollten auf die gleiche Weise gezeichnet werden.

Ein weiterer Vorteil dieser Methode ist, dass keine komplexen statistischen Methoden erforderlich sind und sie auch mit Papier und Bleistift durchgeführt werden können.

Anpassen eines Modells []

Ein praktisches Beispiel für ein kostengünstiges Schülerexperiment, bei dem zwei Modellfunktionen mit Daten verglichen werden, finden Sie hier [1]. Die beiden Modelle entsprechen zwei Funktionen und im Experiment wird geprüft, ob die Daten zu einer dieser Funktionen passen. Diese Anpassung würde zeigen, welches der beiden Modelle die Daten am besten beschreibt.

Literatur

• Kok, K., & Boczianowski, F. (2021). Acoustic Standing Waves: A Battle Between Models. The Physics Teacher, 59(3), 181–184. https://doi.org/10.1119/10.0003659