Handbuch

Typ A []

Wenn Messungen Schwankungen unterworfen sind, sollten wiederholte Messungen durchgeführt werden, um das Messergebnis zu ermitteln (siehe Messwiederholungen). Die Messunsicherheit kann in diesen Fällen mit statistischen Mitteln bestimmt werden. Diese Art der Unsicherheitsbewertung wird als ⓘ Typ ABezeichnet die Unsicherheit eines Messergebnisses, die man durch eine statistische Analyse der Messwerte gewonnen hat.-Unsicherheitsbewertung bezeichnet.

Verringerung der Komplexität []

Die Standardabweichung und die Standardabweichung des Mittelwerts (siehe Unsicherheit) sind die häufigsten Quantifizierungen der Messunsicherheit in der wissenschaftlichen Praxis. Oft haben Lernende Schwierigkeiten, diese zu berechnen und zu interpretieren [1–3]. Um ihnen zu helfen, könnte man den Prozess der Unsicherheitsberechnung automatisieren. Allerdings hat man festgestellt, dass die Lernenden das Gefühl für die Glaubwürdigkeit des Ergebnisses dadurch verlieren [3].

Im Gegensatz dazu, könnte man die Messungen auch grafisch darstellen. Dadurch wird die Variabilität der Messungen visualisiert, was die kognitive Belastung für die Lernenden verringert [4, 5]. Jedoch fehlt bei diesem Ansatz eine numerische Quantifizierung der Unsicherheit, was von Forscher*innen bevorzugt wird und auch in der Schule notwendig ist [1, 3].

Alternative Quantifizierungen []

Eine weitere Möglichkeit besteht darin, andere Quantifizierungen zu verwenden, die leichter zu berechnen und konzeptionell zu verstehen sind. Im Folgenden werden vier alternative Quantifizierungen definiert. Die Forschung hat gezeigt, dass beim Vergleich dieser Quantifizierungen mit der Standardabweichung mit zunehmender mathematischer Komplexität auch die statistische Qualität zunimmt [6].

Die einfachste Quantifizierung ist die maximale Abweichung. Um diese zu berechnen, sortiert man alle Messungen vom kleinsten (x1) zum größten (xN) und berechnet den Mittelwert (x). Die größte Differenz zwischen dem Mittelwert und dem kleinsten bzw. größten Wert der Reihe ist die Unsicherheit: $$u_\text{max} = \max \big( \bar{x} - x_1, x_N - \bar{x} \big).\tag{9}$$ Dieses Maß ist in Abb. 6 grafisch dargestellt. Der Vorteil dieser Quantifizierung ist ihre mathematische Einfachheit. Der Nachteil ist, dass es eine starke Überschätzung der Unsicherheit (im Vergleich zur Standardabweichung) darstellt, die sehr anfällig für Ausreißer ist.


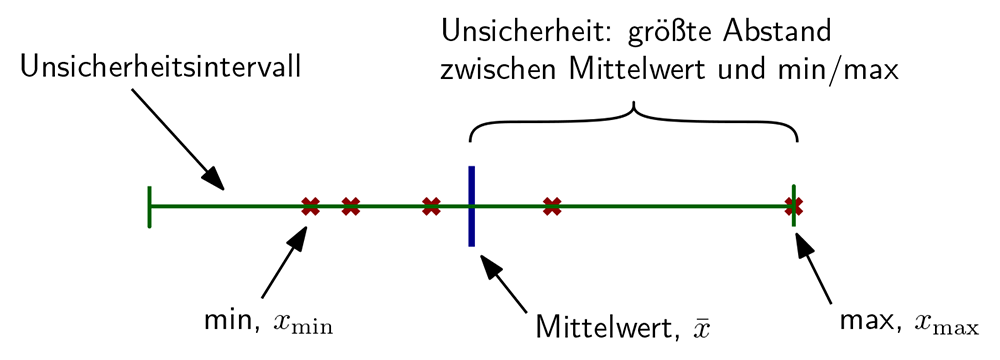
Abbildung 6: Grafische Darstellung der Berechnung der maximalen Abweichung. Die roten Kreuze sind die einzelnen Messungen, der blaue Balken zeigt den Mittelwert an, und die Messunsicherheit ist der größte Abstand zwischen dem Mittelwert und entweder dem Mindest- oder dem Höchstwert des Datensatzes. Der grüne Balken zeigt das gesamte Unsicherheitsintervall um den Mittelwert an.

Um Ausreißer zu kompensieren, kann dieses Verfahren so angepasst werden, dass der kleinste (x1) und der größte (xN) Wert der Reihe ausgeschlossen werden und das Verfahren für die übrigen Messungen wiederholt wird. Dies wird als ausschließen von Extremwerten Quantifizierung bezeichnet: $$u_\text{kein.extr.} = \max \big( \bar{x} - x_2, x_{N-1} - \bar{x} \big).\tag{10}$$ Diese Quantifizierung ist fast so einfach wie die maximale Abweichung, aber weniger empfindlich für Ausreißer. Mit zunehmender Anzahl von Messwiederholungen wird diese Quantifizierung jedoch ebenso empfindlich für Ausreißer.

Bei größeren Stichprobenumfängen könnte man, das Verfahren für die mittlere Hälfte der Messungen anwenden, dies wird als mittlere 50% Verfahren bezeichnet. Dazu werden nach und nach Paare von Extremwerten ausgeschlossen, bis die verbleibende Anzahl von Messungen weniger als die Hälfte der Gesamtzahl der Messungen beträgt. So wird beispielsweise bei 4–7 Messungen ein Paar der Extremwerte ausgeschlossen, bei 8–11 Messungen zwei Paare usw. In Form einer Gleichung kann dies wie folgt geschrieben werden: $$u_\text{mit.50%} = \max \big( \bar{x} - x_{1 + N/4}, x_{N - N/4} - \bar{x} \big).\tag{11}$$ Der Nachteil dieser Maßnahme ist, dass sie für die Lernenden unbefriedigend sein könnte. Sie könnten sich fragen, warum überhaupt wiederholte Messungen durchgeführt wurden, wenn die Hälfte ihres Datensatzes nicht verwendet wird.

Die letzte Alternative ist die mittlere absolute Abweichung (MaA) (Englisch Mean Absolute Deviation, MAD). Dies ist der Durchschnitt der Abweichungen aller Einzelmessungen vom Mittelwert: $$u_\text{MaA} = \frac{1}{N}\sum_{i=1}^N |x_i-\bar{x}|.\tag{12}$$ Da die Berechnung der MaA die Berechnung eines Mittelwerts beinhaltet, ist sie konzeptionell leicht zu verstehen. Diese Unsicherheit ergibt einen Wert, der systematisch kleiner ist als die Standardabweichung.

Weitere Lektüre []

Weitere Informationen zu den verschiedenen Unsicherheitsquantifizierungen und einige Beispiele finden Sie unter [7].

Für einige Ideen für Experimente, bei denen die Analyse der Messunsicherheit eine Notwendigkeit ist, um eine korrekte Schlussfolgerung zu ziehen, siehe [8–14].

Literatur