Handbuch

Vergleich mehrerer Ergebnisse []

Es gibt Fälle, in denen mehr als zwei Datensätze oder Messergebnisse verglichen werden. Hier werden zwei Fälle beschrieben, in denen die Ergebnisse von mehr als zwei Messergebnissen verglichen und die Beziehung zwischen zwei Größen anhand von Graphen analysiert werden (siehe auch Graphen).

Vergleich von drei Messergebnissen []

In Abschnitt Einfacher Vergleich wurde der Prozess des Vergleichs zweier Datensätze oder Messergebnisse durchgeführt. Man kann dasselbe Verfahren auch anwenden, um die Ergebnisse von drei Messungen zu vergleichen. Allerdings muss man bei der Interpretation der Ergebnisse sehr vorsichtig sein.

Angenommen, die Viskosität von drei verschiedenen Flüssigkeiten A, B und C wird gemessen (siehe Abb. 11). Wenn man die Viskosität der Flüssigkeiten vergleicht, muss man zu dem Schluss kommen, dass die Viskosität von Flüssigkeit A sowohl mit C als auch mit B verträglich ist. Man kann jedoch nicht zu dem Schluss kommen, dass das Ergebnis von Flüssigkeit B mit Flüssigkeit C verträglich ist—obwohl beide mit Flüssigkeit A verträglich sind.

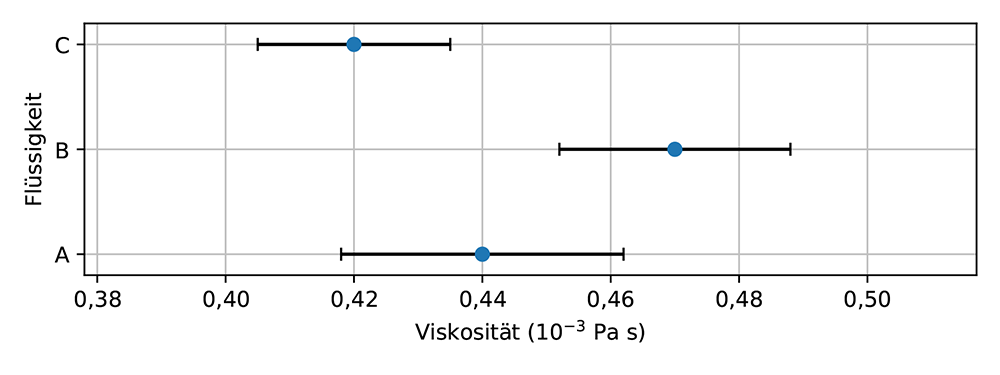
Abbildung 11: Die Messergebnisse für die Viskosität von drei Flüssigkeiten.

Darüber hinaus kann aus den Ergebnissen geschlossen werden, dass die Viskosität von Flüssigkeit C niedriger ist als die Viskosität von Flüssigkeit B. Für die Flüssigkeit A beschränkt sich die Schlussfolgerung darauf, dass ihre Viskosität sowohl mit der von B als auch mit der von C verträglich ist. Will man eine ausführlichere Aussage über die Viskosität der Flüssigkeit A treffen, müssen die Unsicherheiten verringert werden.

Analyse von Fitfunktionen []

Oft werden mehrere Messungen durchgeführt, um die Zusammenhang zwischen zwei Größen zu untersuchen. Bei der Datenanalyse wird beurteilt, ob die beiden Größen einem bestimmten Modell oder einer bestimmten Gleichung entsprechen. Diese Daten können in tabellarischer Form ausgewertet werden, aber gegebenenfalls ist es einfacher, die Ergebnisse in grafischer Form zu interpretieren [1, 2]. In Graphen wurde das Verfahren zum Zeichnen von Fitfunktionen und deren Unsicherheiten beschrieben. In diesem Abschnitt geht es um die Interpretation dieser Fitfunktionen.

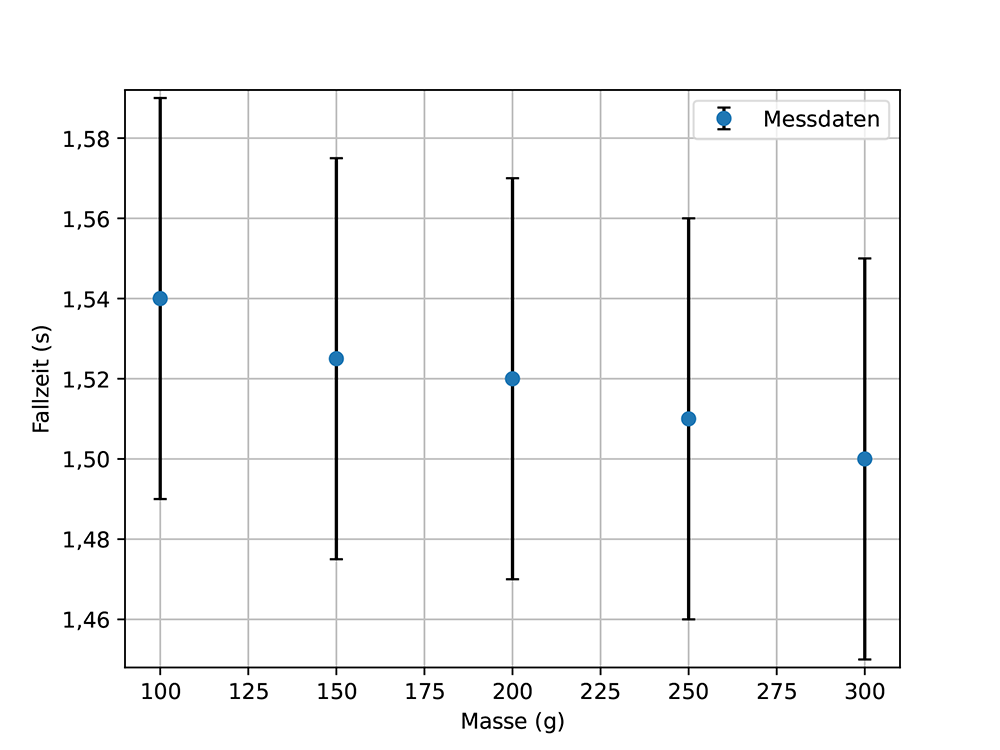
Um die Frage zu beantworten, ob schwerere Objekte schneller fallen als leichtere, könnte man ein Experiment durchführen. In Abb. 12a sind die Fallzeiten von Kugeln unterschiedlicher Masse dargestellt. Die Frage ist nun, ob die Masse die Fallzeit beeinflusst oder nicht.

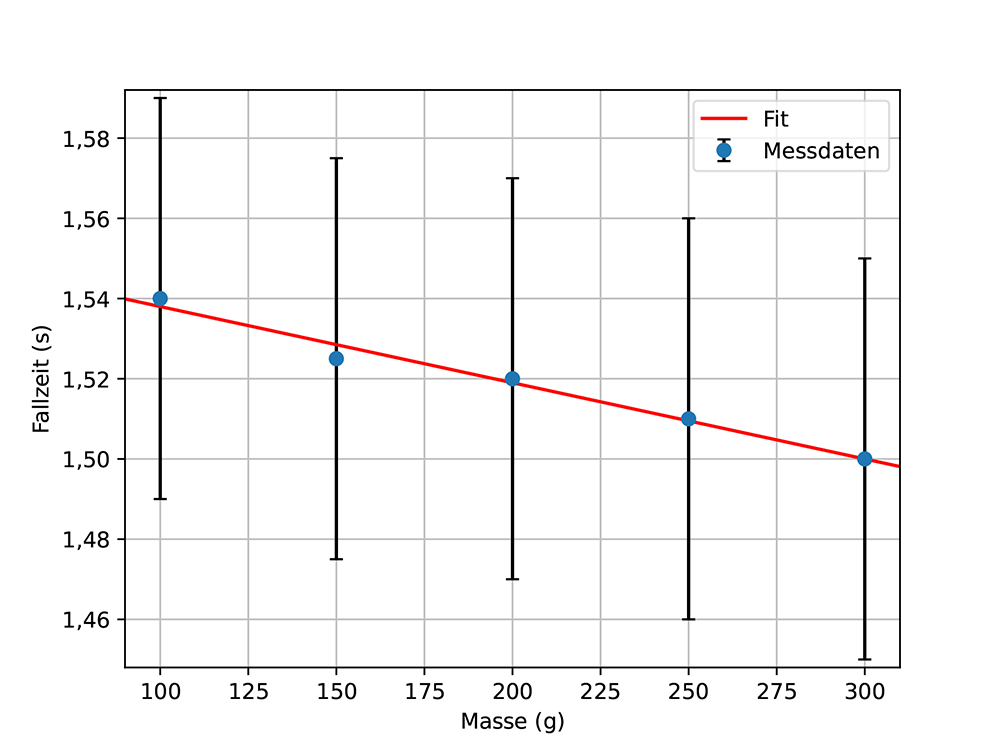
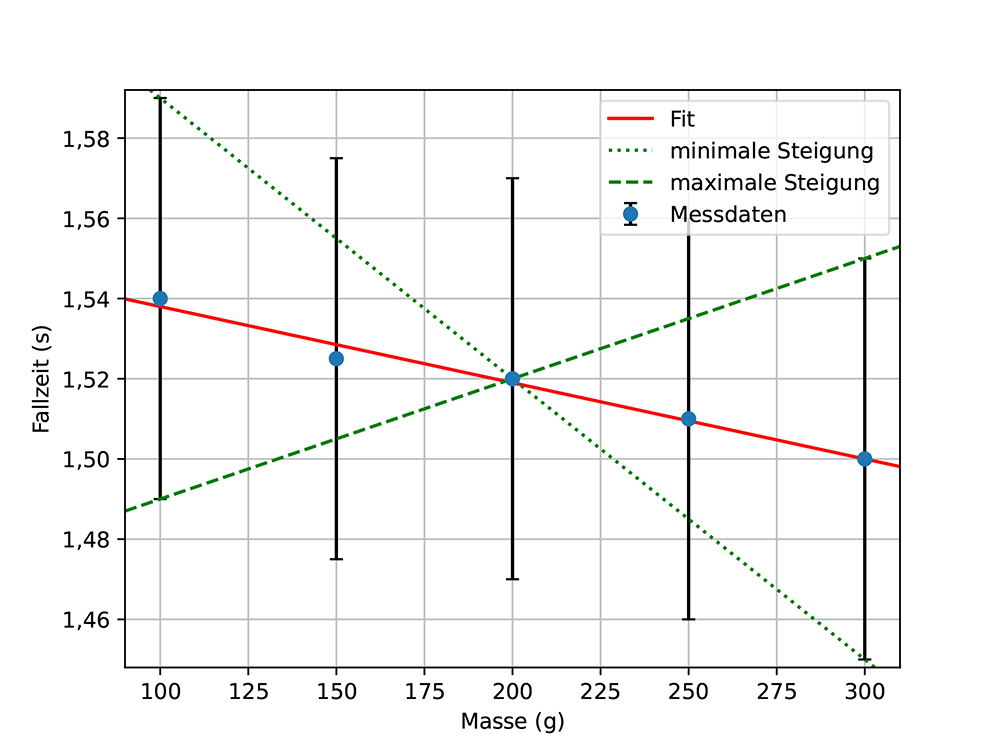
Auf den ersten Blick scheinen die Daten eine Abnahme der Fallzeit mit zunehmender Masse zu zeigen. Dies geht auch aus der Fitfunktion hervor, siehe Abb. 12b. Betrachtet man jedoch die maximale und minimale Steigung, siehe Abb. 12c, so wird deutlich, dass sowohl positive als auch negative Steigungen mit den Daten übereinstimmen. Die Schlussfolgerung ist, dass aufgrund der Möglichkeit positiver und negativer Steigungen kein Einfluss der Masse auf die Fallzeit angenommen werden kann. Es ist zu beachten, dass diese Schlussfolgerung erst nach der Unsicherheitsanalyse gezogen werden konnte.

Wenn man den Einfluss der Reibung auf kleinere Massen zeigen will, was zu längeren Fallzeiten für kleinere Massen führen würde, müssten die Unsicherheiten drastisch reduziert werden.

1 / 3
(a) Fünf Zeitmessungen der Fallzeit von Kugeln mit unterschiedlichen Massen.
2 / 3
(b) Die rote Linie zeigt eine lineare Fitfunktion für die Daten.
3 / 3
(c) Die grün gestrichelten Linien zeigen die minimale und maximale Steigung der Fitfunktion an.
❮ ❯

Abbildung 12: Die Messergebnisse eines Experiments, bei dem Kugeln mit unterschiedlicher Masse aus einer bestimmten Höhe fallen gelassen werden.

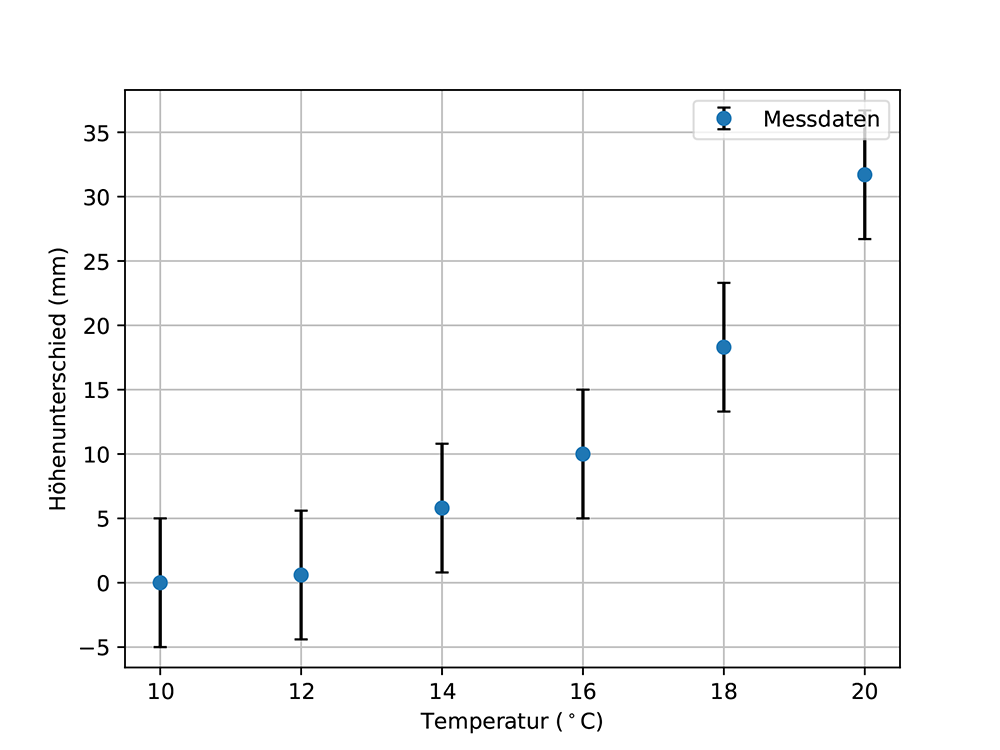
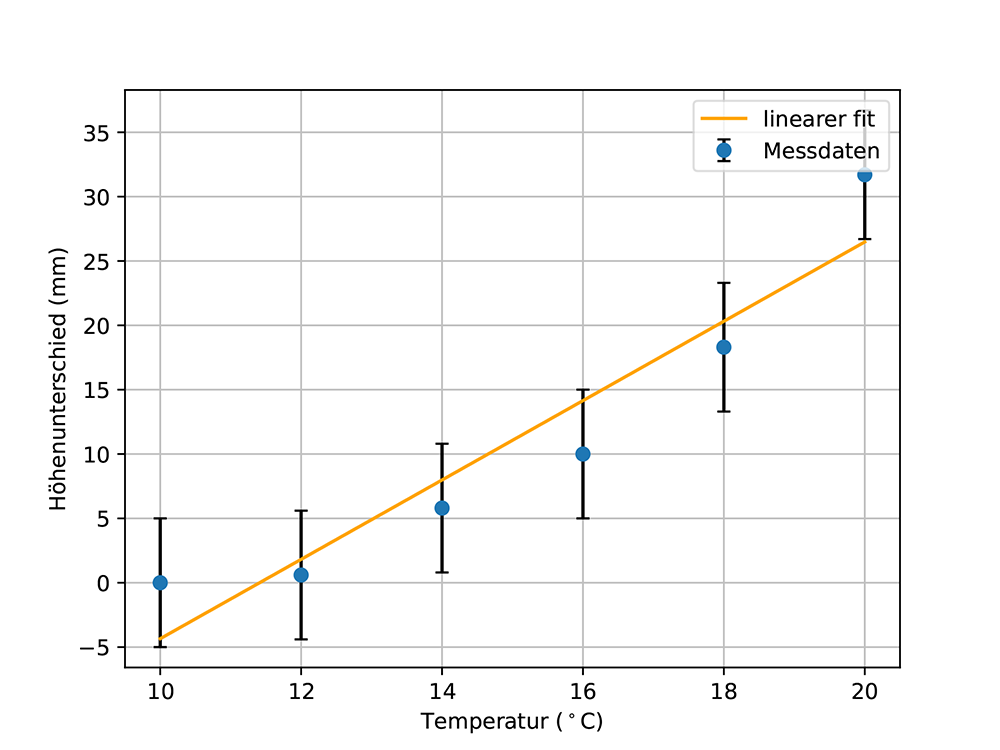
Wenn man sich für die thermische Ausdehnung von Wasser interessiert, kann man die Abhängigkeit der Volumenänderung von der Temperatur untersuchen. Dazu kann man ein Experiment durchführen, bei dem die Höhe einer Wassersäule bei verschiedenen Temperaturen gemessen wird, siehe Abb. 13a. Die Anfangshöhe beträgt 0 mm bei einer Anfangstemperatur von 1ºC und die Temperatur wird langsam in Schritten von 2°C bis zu einer Temperatur von 20°C erhöht, siehe Abb. 13b.

1 / 5
(a) Messung der Höhe der Wassersäule bei verschiedenen Temperaturen.
2 / 5
(b) Messergebnisse für die Ausdehnung von Wasser.
3 / 5
(c) Eine lineare Fitfunktion für die Daten.
4 / 5
(d) Eine quadratische Fitfunktion für die Daten.
5 / 5
(e) Präzisere Messergebnisse.
❮ ❯

Abbildung 13: Einige experimentelle Daten zur Ausdehnung eines Wasservolumens bei verschiedenen Temperaturen.

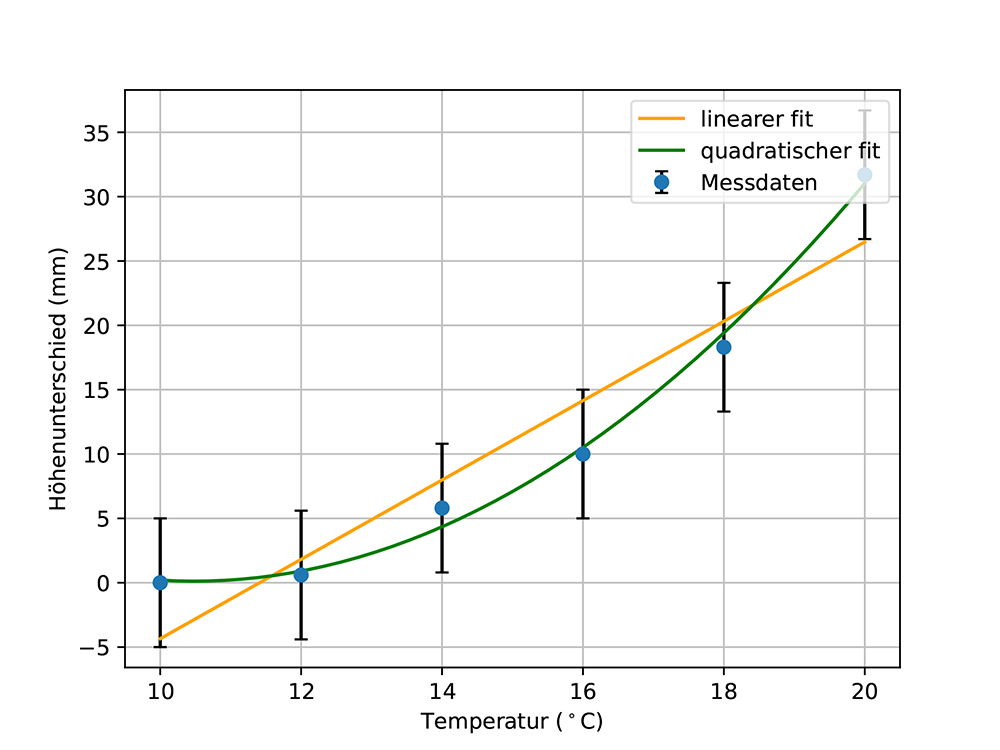
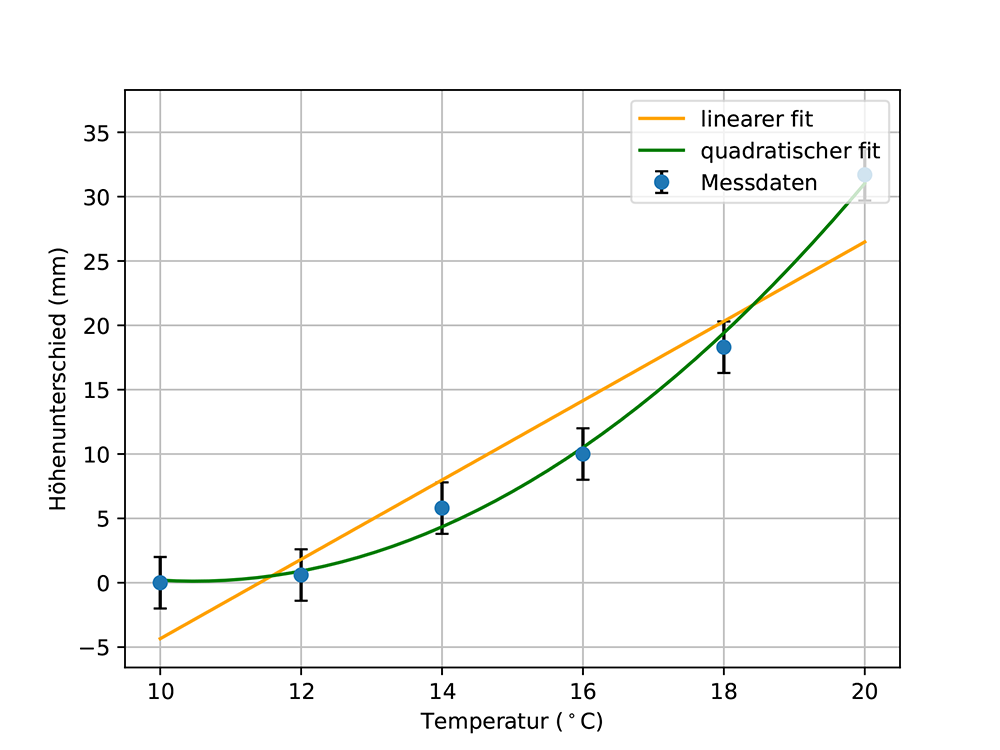
In einem ersten Schritt wird eine lineare Fitfunktion erstellt, siehe Abb. 13c. Diese Fitfunktion geht durch alle Unsicherheitsbalken und passt daher zu den Daten. Obwohl eine quadratische Funktion besser zu den Daten passt, siehe Abb. 13d, kann eine lineare Abhängigkeit nicht ausgeschlossen werden. Wenn man das Experiment verfeinert und die Unsicherheiten verringert, siehe Abb. 13e, ist man schließlich in der Lage, eine lineare Abhängigkeit zu falsifizieren und eine quadratische Abhängigkeit wahrscheinlicher zu machen.

Weitere Lektüre []

Eine ausführlichere Beschreibung und Analyse der thermischen Ausdehnung von Wasser findet sich hier [3].

Literatur